Cálculo
-3 multiplicaciones, 2 divisiones.
Problemas
1 problema para resolver
1 problema para inventar
Ejercicios dictados
a) Composición y descomposición en base 10.
b) Potencias.
-3 multiplicaciones, 2 divisiones.
Problemas
1 problema para resolver
1 problema para inventar
Ejercicios dictados
a) Composición y descomposición en base 10.
b) Potencias.
Etiquetas:
tareas
![]()
Tareas. Matemáticas
Cálculo (4 multiplicaciones) (2 divisiones).
Problemas (1 problema para resolver) (1 problema para inventar con una operación combinada).
Inicio de la unidad 2
-Los múltiplos de un número.
Pág 28 nº 1 al 3
Cálculo (4 multiplicaciones) (2 divisiones).
Problemas (1 problema para resolver) (1 problema para inventar con una operación combinada).
Inicio de la unidad 2
-Los múltiplos de un número.
Pág 28 nº 1 al 3
Etiquetas:
tareas
![]()
Etiquetas:
tareas
![]()
Repaso. Lengua
-Sinónimos y antónimos.
pág. 31 del 1 al 4
-Clases de sustantivos.
pág. 32 nº 1
pág. 33 nº 2 y 3.
-Sinónimos y antónimos.
pág. 31 del 1 al 4
-Clases de sustantivos.
pág. 32 nº 1
pág. 33 nº 2 y 3.
Etiquetas:
tareas
![]()
Repaso de la unidad.
Deberes dictados.
-Problemas (2).
-Cálculo (4 multiplicaciones, 4 divisiones).
-Ejercicio de redondeo.
Para recordar el redondeo pulsa aquí
Deberes dictados.
-Problemas (2).
-Cálculo (4 multiplicaciones, 4 divisiones).
-Ejercicio de redondeo.
Para recordar el redondeo pulsa aquí
Etiquetas:
tareas
![]()
Repasamos: Cómo resolver divisiones de tres cifras.

Antes de comenzar a dividir es importante que sepas las tablas de multiplicar, porque las vamos a utilizar para resolver la división. Si no recuerdas las tablas de multiplicar puedes repasarlas en el siguiente enlace: tablas de multiplicar.
Una vez repasadas las tablas podemos empezar a hacer la división de 3 cifras. Los pasos que debemos seguir son los siguientes:
1. Como el divisor tiene 3 cifras debemos tomar las 3 primeras cifras del dividendo.
2. Comparamos las 3 cifras de dividendo con las 3 cifras del divisor:
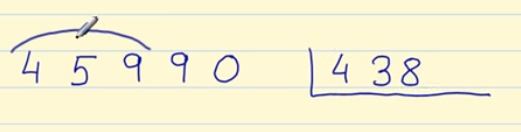
Tomamos las 3 primeras cifras y las comparamos con el divisor:
Como 459 es mayor que 438, podemos empezar a hacer la división
3. Dividimos las cifras del dividendo entre las cifras del divisor.

Para dividir 459 entre 438 tomamos la primera cifra de cada número y las dividimos: 4 : 4 = 1
Escribimos el 1 en el cociente y lo multiplicamos por el divisor: 438 x 1 = 438.
Escribimos el resultado debajo y restamos: 459 – 438 = 21
4. Bajamos la siguiente cifra y volvemos a dividir.

Bajamos el 9 que es la cifra siguiente del dividendo. Ahora dividimos 219 entre 438.
Pero no se puede dividir porque 219 es más pequeño que 438.
5. Si la cifra del dividendo es más pequeña que el divisor debemos bajar otra cifra más.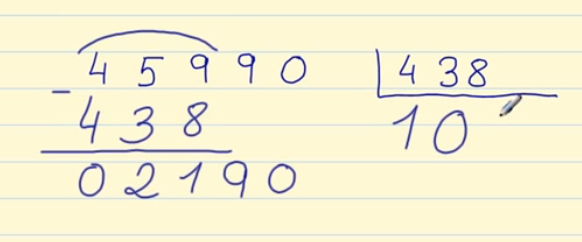
Como no se puede dividir 219 entre 438, escribimos un cero en el cociente y bajamos la cifra siguiente.
En este caso bajamos el cero.
Ahora nos toca dividir 2190 entre 438, que sí se puede.
6. La división termina cuando no haya más cifras en el dividendo para bajar.

Dividimos las dos primeras cifras del dividendo entre la primera del divisor: 21 : 4 = 5
Escribimos 5 en el cociente y multiplicamos por el divisor:
438 x 5 = 2190
Escribimos 2190 debajo del 2190 y restamos:
2190 – 2190 = 0
Como no tenemos más cifras para bajar, hemos terminado la división:
45990 : 438 = 105; resto=0
Ahora practica aquí

Antes de comenzar a dividir es importante que sepas las tablas de multiplicar, porque las vamos a utilizar para resolver la división. Si no recuerdas las tablas de multiplicar puedes repasarlas en el siguiente enlace: tablas de multiplicar.
Una vez repasadas las tablas podemos empezar a hacer la división de 3 cifras. Los pasos que debemos seguir son los siguientes:
1. Como el divisor tiene 3 cifras debemos tomar las 3 primeras cifras del dividendo.
2. Comparamos las 3 cifras de dividendo con las 3 cifras del divisor:
- Si el número de 3 cifras de dividendo es mayor que el número del divisor podremos empezar a dividir.
- Si el número de 3 cifras del dividendo es menor que el número del divisor tienes que tomar la cifra siguiente del dividendo. Ahora tienes 4 cifras en el dividendo.
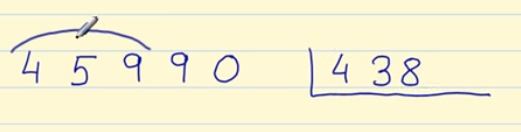
Tomamos las 3 primeras cifras y las comparamos con el divisor:
Como 459 es mayor que 438, podemos empezar a hacer la división
3. Dividimos las cifras del dividendo entre las cifras del divisor.

Para dividir 459 entre 438 tomamos la primera cifra de cada número y las dividimos: 4 : 4 = 1
Escribimos el 1 en el cociente y lo multiplicamos por el divisor: 438 x 1 = 438.
Escribimos el resultado debajo y restamos: 459 – 438 = 21
4. Bajamos la siguiente cifra y volvemos a dividir.

Bajamos el 9 que es la cifra siguiente del dividendo. Ahora dividimos 219 entre 438.
Pero no se puede dividir porque 219 es más pequeño que 438.
5. Si la cifra del dividendo es más pequeña que el divisor debemos bajar otra cifra más.
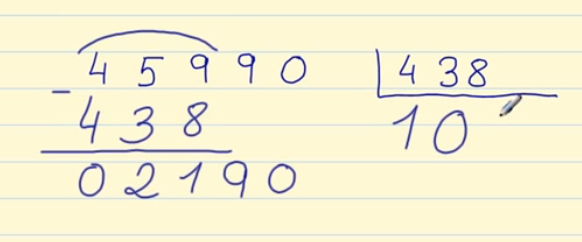
Como no se puede dividir 219 entre 438, escribimos un cero en el cociente y bajamos la cifra siguiente.
En este caso bajamos el cero.
Ahora nos toca dividir 2190 entre 438, que sí se puede.
6. La división termina cuando no haya más cifras en el dividendo para bajar.

Dividimos las dos primeras cifras del dividendo entre la primera del divisor: 21 : 4 = 5
Escribimos 5 en el cociente y multiplicamos por el divisor:
438 x 5 = 2190
Escribimos 2190 debajo del 2190 y restamos:
2190 – 2190 = 0
Como no tenemos más cifras para bajar, hemos terminado la división:
45990 : 438 = 105; resto=0
Ahora practica aquí
Etiquetas:
divisiones,
matemáticas
![]()
Ordena de mayor a menor estas cantidades:
a) 6,834.980
b) 3x10 (6) +7x10(5) + 2 x10 (4) +3
c) 4x100(2)
d) 3 x10 (6) + 7 x10 (4) + 3 x 10(3) + 9 x 10 + 9
Problemas
Pág. 21 nº del 4 al 6.
a) 6,834.980
b) 3x10 (6) +7x10(5) + 2 x10 (4) +3
c) 4x100(2)
d) 3 x10 (6) + 7 x10 (4) + 3 x 10(3) + 9 x 10 + 9
Problemas
Pág. 21 nº del 4 al 6.
Etiquetas:
tareas
![]()
Descomponer números en potencias de base 10
Si nos fijamos bien estoy seguro que no tendremos problemas para descompner cualquier número. Es importante que entiendas bien las potencias de base 10.
Así por ejemplo 3000 es igual que 3x1000 y esto a su vez es lo mismo que 3x103.
Para practicar vamos a hacer los ejercicios:
-Pág 19 nº 42 al 45.
Si nos fijamos bien estoy seguro que no tendremos problemas para descompner cualquier número. Es importante que entiendas bien las potencias de base 10.
Así por ejemplo 3000 es igual que 3x1000 y esto a su vez es lo mismo que 3x103.
Para practicar vamos a hacer los ejercicios:
-Pág 19 nº 42 al 45.
Etiquetas:
tareas
![]()
-Azucena toma dos pastillas por la mañana, cuatro después de comer y tres por la noche. ¿Cuántas
pastillas toma a la semana? Utiliza la propiedad distributiva para resolver el problema.
-Ángel ha pedido al almacén para su papelería 625 bolígrafos azules. El almacén le envía 5 palés, con 5 cajas cada uno y dentro de cada caja, 5 estuches con 5 bolígrafos. Escribe el problema en forma de potencia.
-Pág.19 del 39 al 41.
-Traer para mañana una caja de palillos redondos y un bloque de plastilina pequeño (da igual el color).
pastillas toma a la semana? Utiliza la propiedad distributiva para resolver el problema.
-Ángel ha pedido al almacén para su papelería 625 bolígrafos azules. El almacén le envía 5 palés, con 5 cajas cada uno y dentro de cada caja, 5 estuches con 5 bolígrafos. Escribe el problema en forma de potencia.
-Pág.19 del 39 al 41.
-Traer para mañana una caja de palillos redondos y un bloque de plastilina pequeño (da igual el color).
Etiquetas:
tareas
![]()
Decoración de Halloween: Botes decorados

Aqui va otra posible decoración para Halloween.
Tan sólo necesitaremos:
- Unos botes de cristal
- Tijeras
- Un poco de cola
- Papel pinocho ó papel crepé (blanco y naranja)
- Cartulina color negro
- Velas
Hemos de forrar los botes de cristal con el papel naranja para hacer calabazas y con el papel blanco
si queremos hacer unos fantasmas. Intante no poner demasiada cola en el cristal, porque sino se humedecerá
demasiado el papel y puede llegar a romperse.
Una vez tengamos los botes forrados de papel pinocho color naranja ó color blanco bien secos,
utilizaremos la cartulina negra, para hacer la forma de los ojos, boca y dientes. Después de recortar estas
formas las pegaremos al papel.
Por último pondremos una vela encendida dentro del bote de cristal.
Otros diseños:
pdf del fantasma- cadavera- murciélago calabaza.



Etiquetas:
halloween,
plástica
![]()
POTENCIAS
Actividad web que nos permite convertir una multiplicación de factores iguales en una potencia.
Actividad web que nos permite convertir una multiplicación de factores iguales en una potencia.


Etiquetas:
Juegos mate,
potencias
![]()
Repaso de las potencias.
Pág. 16 nº 27 y 28.
Pág 17 nº 29 y 30.
Resuelve:
3x3x3x3=
4x4=
5x5x5x5x5=
6(3)=
9(1)=
10(5)=
Inventa un problema con 6(3)=
Pág. 16 nº 27 y 28.
Pág 17 nº 29 y 30.
Resuelve:
3x3x3x3=
4x4=
5x5x5x5x5=
6(3)=
9(1)=
10(5)=
Inventa un problema con 6(3)=
Etiquetas:
tareas
![]()
Origami es el es el arte de origen japonés del plegado de papel, que en español también se conoce como ‘papiroflexia’ o “hacer pajaritas de papel”. La diferencia principal con el Kirigami es que el Kirigami es el arte del papel recortado mientras que el Origami lo es del papel plegado.
Aquí os dejo un ejemplo.
Con un papel, unos dobleces y unos cortes las posibilidades son infinitas pero…. debemos empezar por cosas sencillas. En la página http://www.origami-resource-center.com/ encontrarás todo un mundo del origami y kirigami con patrones para construir. Vamos a para empezar con cortes sencillos :
Instrucciones: Dobla un folio o cartulina a la mitad y realiza dos cortes donde realizaste el doblez. Pliega la zona entre cortes hacia la derecha (figura 2). Vuelve a colocar de nuevo ese corte hasta su posición inicial (figura 3). Empuja ese corte hacia dentro de la página y voilá ya lo tienes. Desdobla la hoja y verás el resultado.
Diferentes formas de los cortes abren un sinfín de posibilidades.
También puedes encontrar otros ejemplos en la página de Cercle Cromátic en el apartado construcciones tridimensionales (muy interesante). Para muestra un botón:

Etiquetas:
plástica
![]()
Suscribirse a:
Comentarios (Atom)










































